Heinz Schumann
Computerunterstützes Entdecken und Lösen
geometrischer Extremwertaufgaben in der Sekundarstufe I
| Durch eine andere Behandlung erfährt so manches eine Wandlung. |
1. Einleitung
Noch in den 70er Jahren gehörte die Behandlung von Extremwertaufgaben, die sich auf quadratische Zielfunktionen zurückführen lassen, zum Aufgabenrepertoire des Mathematikunterrichts in Klasse 9. -Vorbildlich ist eine solche Behandlung durchgeführt z. B. im Unterrichtswerk Plus, 9. Schuljahr (Schönbeck/Schupp 1978). -Wie auch andere mathematische Inhalte, sind solche Mathematikaufgaben den Stundentafelkürzungen zum Opfer gefallen, obwohl diese eine motivierende Anwendung der quadratischen Funktionen darstellen, die auch bei den entsprechenden schriftlichen Abschlußprüfungen berücksichtigt werden könnten und sollten. (Eine rühmliche Ausnahme macht in diesem Zusammenhang der Mathematikunterricht im Freistaat Bayern.)
In der neueren didaktischen Diskussion wurde - im Gegensatz zur genannten curricularen Fehlentwicklung - sogar die Forderung nach der Behandlung "nichtquadratischer" Extremwertaufgaben in der Sekundarstufe I erhoben (u. a. Dörr 1989, Glatfeld 1989, Schulz 1989, Schupp 1997). –Erst folgende Autoren benutzten konsequent andere Computerwerkzeuge als Tabellenkalkulationssysteme zur Lösung von Extremwertaufgaben in der Sekundarstufe I: Schumann (1991/92), Appel (1993), Rüthing (1998).
Unter Verwendung aktueller Computerwerkzeuge für die dynamische Geometrie und unter Verwendung von Computeralgebra werden wir diese Diskussion weiterführen, indem wir eine Konzeption für die computerunterstützten Behandlung geometrischer Extremwertaufgaben entwickeln, die sich auf allgemeinere Zielfunktionen als die quadratischen zurückführen lassen.
2. Computerunterstützte Behandlungsmethoden für Extremwertaufgaben
Wir beginnen mit einer Kritik der üblichen Aufgabenstellung von Extremwertaufgaben: Die Aufgabenstellung geht immer schon von der Existenz eines Extremums aus, obwohl gerade die Entdeckung, dass es überhaupt ein Maximum oder Minimum gibt, ein Erkenntnisakt für sich ist. Es ist deshalb erstens in einer gesonderten Aufgabenstellung die Untersuchung einer geometrischen Figur auf extremale Eigenschaften hin vorzunehmen. Zweitens ist die festgestellte extremale Eigenschaft in Form einer Berechnungsaufgabe zu formulieren. Drittens ist diese Berechnungsaufgabe (exakt) zu lösen.
Eine adäquate Modellierung geometrischer Figuren zur Untersuchung auf extremale Eigenschaften hin bieten die dynamische Geometriewerkzeuge. (Wir verwenden hier das geometrieinhaltliche und software-ergonomisch vorbildhafte Cabri-Géomètre.)
Folgende experimentelle Methode zur Entdeckung von Extremwertaufgaben als Berechnungsaufgaben, die auch eine näherungsweise Bestimmung von Extremwerten per Augenmaß gestattet, kommt zur Anwendung (Schumann 1998):
| (1) | Konstruktion einer geometrischen Figur, die auch Nebenbedingungen erfüllt |
| (2) | Variation einer unabhängigen Größe der Figur bzw. Teilfigur unter Beobachtung eines funktionalen Zusammenhangs: unabhängige Größe - abhängige Größen (Datensammlung in Werte-Tabelle; grafische Darstellung im Schaubild) |
| (3 | Erkennen einer extremalen Eigenschaft (näherungsweises Bestimmen von Extremstelle und Extremwert) |
| (4) | Variation der Figurenparameter und Prüfung, ob extremale Eigenschaft invariant |
| (5) | Formulierung einer geometrischen Extremwertaufgabe als Berechnungsaufgabe |
Diese Methode ist präformal, da sie im allgemeinen nicht das Aufstellen einer Zielfunktion notwendig macht, aber trotzdem gestattet, die Zielfunktion als eine quasi empirische Funktion auf extremale Eigenschaften hin zu untersuchen.
Da wir allenfalls davon ausgehen können, daß die Schüler und Schülerinnen Novizen in der Nutzung eines geometrischen Computerwerkzeugs sind, stellen wir die Bildschirm-Konfiguration zusammen mit den Aufgabentexten als "interaktive Arbeitsblätter" (Schumann 1998), die auch zu Demonstrationszwecken verwendet werden können, zur Verfügung. Der Einsatz solcher Arbeitsblätter bietet einen ersten Zugang zur dynamischen Behandlung von geometrischen Extremwertaufgaben.
Die Verwendung von Tabellenkalkulationsprogrammen zur experimentellen Behandlung geometrischer Extremwertaufgaben oder Extremwertaufgaben, die sich geometrisch modellieren lassen, halten wir u.a. aus folgenden Gründen für nicht besonders geeignet:
Für das Lösen der formulierten Extremwertaufgabe als Berechnungsaufgabe verwenden wir zur Reduktion des Berechnungsaufwands die Computeralgebra-Komponente von Derive. Das Aufstellen und Bearbeiten der Zielfunktion ist aber ein heuristischer Prozeß , bei dem die Computeralgebra nur unterstützend wirken kann. - Wie nun bei nichtquadratischen Zielfunktionen die Extremstelle bestimmen, ohne den Kalkül der Differentialrechnung zu verwenden? Die Ungleichung vom arithmetischen und geometrischen Mittel ist doch ein probates und elementares Werkzeug zur Lösung von Extremwertaufgaben? Sie müßte aber für einen solchen Einsatz in der Sekundarstufe I erst bereitgestellt werden (wo doch heute schon Extremwertaufgaben Zusatzstoff sind!). Ihre betreffende Anwendung ist zudem für die Schüler und Schülerinnen recht ungewohnt, fallweise ziemlich kompliziert und nicht algorithmisierbar. Wir geben deshalb eine Lösungsmethod an, die besser in den Kontext des üblichen Mathematikunterrichts in der Sekundarstufe I passt, die zudem gewisse infinitesimale Überlegungen in der Sekundarstufe II präfiguriert und die von mathematikunterrichtsgeschichtlicher Bedeutung ist.
Exkurs:
Es sei x ® f(x) eine stetige Funktion, für die in xm ein lokales Extremum existiert und die in xm differenzierbar ist.

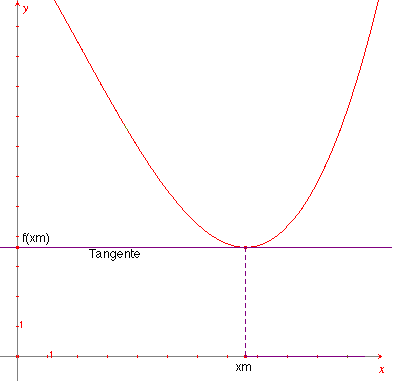
Abb. 1
Im Extrempunkt (xm; f(xm)) existiert eine horizontale Tangente (Abb. 1), die auf dreierlei Art systematisch als Grenzlage einer Sekante angesehen werden kann (Abb. 2 a/b, 3 a/b, 4 a/b). Alle drei Fälle führen zu einer elementarisierten Berechnung der Extremstelle xm.
Die erste Möglichkeit (Abb. 2 a/b), bei der die Sekante durch den Extremalpunkt geht, illustriert die Methode nach der Fermat (1601-1655) die Extremstelle bestimmt: Es ist f(xm+d) - f(xm) » 0 für ein "hinreichend kleines d"; Division dieser "Gleichung" durch d ¹ 0 führt auf eine wesentliche Gleichung, in der dann d=0 für den Grenzübergang (Grenzlage der Sekante) zu setzen ist.
Bei der zweiten Möglichkeit (Abb. 3 a/b) geht die Sekante durch zwei Punkte der
Funktionskurve, deren x-Koordinaten äquidistant zur Extremstelle liegen: Es ist f(xm+d) - f(xm-d) » 0 für ein hinreichend kleines d; nach Dvision mit d wird der Grenübergang durch Setzen von d=0 vorgenommen; man erhält eine Bestimmungsgleichung für xm.
Eine horizontale Sekante wird bei der dritten Möglichkeit gewählt (Abb. 4 a/b): Es ist
f(x+d) - f(x-d) = 0; Division mit d ¹ 0 führt auf eine wesentliche Gleichung, die äußerlich mit der aus der vorstehenden Möglichkeit übereinstimmt; mit d=0 erhält man
eine Bestimmungsgleichung für xm. Diese Methode geht auf Schellbach (1804-1892) zurück. (Bei ganz rationalen Funktionstermen reduziert sich durch die Differenzbildung f(x + d) - f(x - d) der Grad um 1, so daß Extremwertaufgaben mit ganz rationalen Zielfunktionen bis zum Grad 5 exakt gelöst werden können. Bei gebrochen rationalen Zielfunktionen läßt sich die Bestimmungsgleichung ganz rational machen. Schwieriger verhält es sich natürlich bei (Quadrat-) Wurzelfunktionen als Zielfunktionen usw.)
In allen drei Fällen liefert die Bestimmungsgleichung natürlich nur jene Stellen, in denen eine horizontale Tangente existiert. Es sind jene Stellen auszuwählen, für die durch unser Vorgehen schon vorher gesichert ist, dass sie Extremstellen sind.
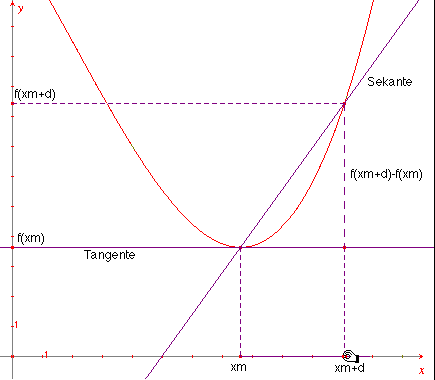
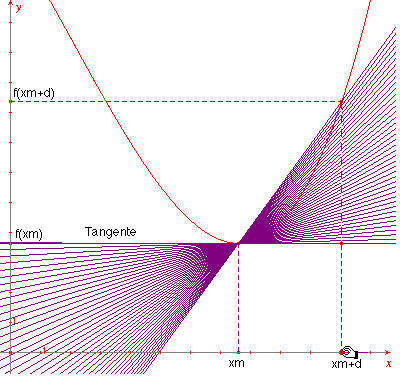 Abb. 2 a
Abb. 2 a
Abb. 2 b

Abb. 3 a
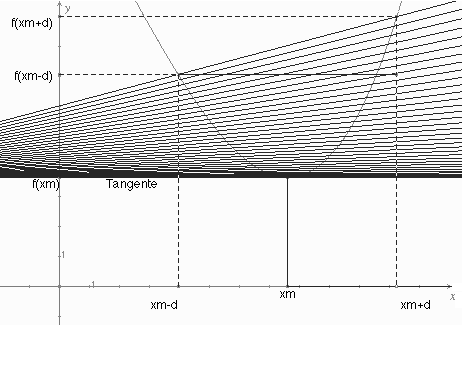
Abb. 3 b

Abb. 4 a
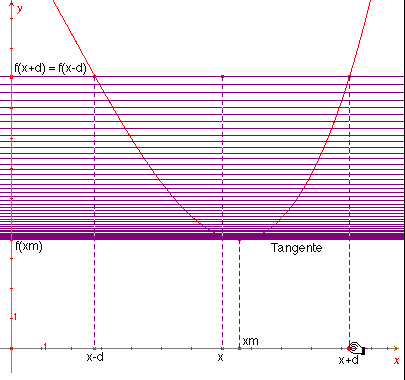
Abb. 4 b
Im folgenden verwenden wir die Methode von Schellbach, da sie den Schülern gut verständlich gemacht werden kann und da sie von einer Gleichung ausgeht und deshalb die Voraussetzung "für ein hinreichend kleines d" bzw. "in einer hinreichend kleinen Umgebung von xm" vermeidet.
Folgende Methode zur Berechnung von Extremstellen und Extremwerten ("Differenzmethode" nach Schellbach) ergibt sich:
| (1) | Aufstellen der Zielfunktion mit dem Funktionsterm f(x) (auch unter Berücksichtigung einer Nebenbedingung) |
| (2) | Gleichung f(x + d) - f(x - d) = 0 bilden |
| (3) | Ausklammern von d und Division durch d ¹ 0 |
| (4) | Gewinnen der Bestimmungsgleichung für xm: d gleich Null setzen |
| (5) | Exaktes (oder näherungsweises) Lösen der Bestimmungsgleichung |
| (6) | Berechnen des Extremwertes durch Einsetzen von xm in f (x) (Prüfung zulässiger Lösungen im Aufgabenkontext) |
| (7) | Berechnen weiterer gesuchter Größen. |
Wir wenden nun die in der Einleitung skizzierten Methoden auf zwei Beispiele an, eines ohne, das andere mit Nebenbedingung.
Eine Vorbemerkung: Sowohl bei der Behandlung mit dynamischer Computergeometrie als auch bei der Behandlung mit Computeralgebra gehen wir nur soweit auf die Werkzeuge ein, wie es uns für das Verständnis notwendig scheint. Für weitergehende Informationen verweisen wir auf die entsprechenden Handbücher.
Beispiel 1 (Volumen einer nach oben offenen Schachtel)
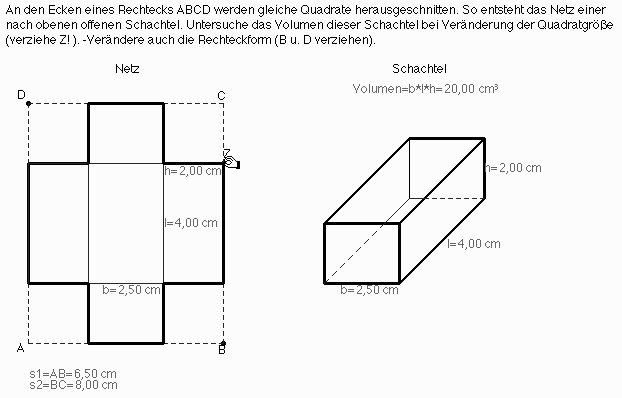
Abb. 5
Die Abbildung 5 zeigt ein interaktives Arbeitsblatt, anhand dessen der Schüler/die Schülerin erst einmal feststellen kann, daß das Schachtelvolumen sich in Abhängigkeit von der Größe der herausgeschnittenen Quadrate ändert; der Handcursor symbolisiert dabei den zu verziehenden Punkt, mit dem der Wert der unabhängigen Variablen variiert wird (Abb. 6).
Bereits jetzt kann herausgefunden werden, daß das Volumen vermutlich zwischen
h = 0 und h = s1 ein Maximum annimmt. Um die Daten der unabhängigen Größe h und die zugehörigen Daten des von ihr abhängigen Volumens zu analysieren, können diese während der Änderung von h in eine Tabelle eingetragen werden (Abb. 7). Es erhärtet sich die Vermutung, daß zwischen den Randwerten von h ein Maximum angenommen wird.
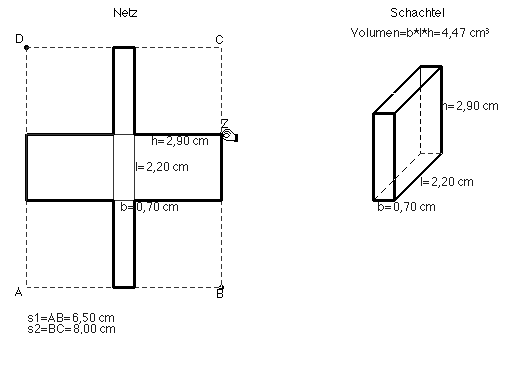 Abb. 6
Abb. 6
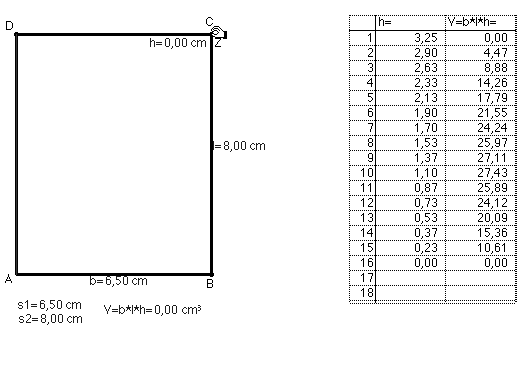 Abb. 7
Abb. 7
Gewissheit über die Existenz nur eines Maximums erhält man durch ein Schaubild für die Funktion h ® V(h) als Spur des Punktes (h, V(h)), wenn h am Netz variiert wird (Abb. 8).
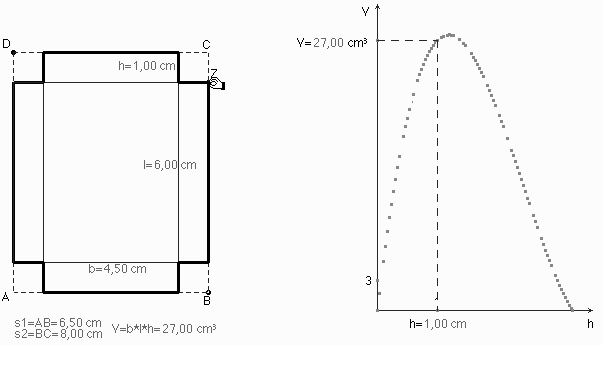 Abb. 8
Abb. 8
Die Kurve des Schaubildes entsteht vor den Augen der Schüler als Verbindungslinie vieler Punkte (Brückenlinie). Die Spur, nur ein Bildschirmzustand, kann durch ein referenzierbares grafisches Objekt ersetzt werden, an dem das Maximum nach Augenmaß recht gut abgelesen werden kann: hmax » 1,20 cm, Vmax » 27,55 cm3 (Abb. 9).
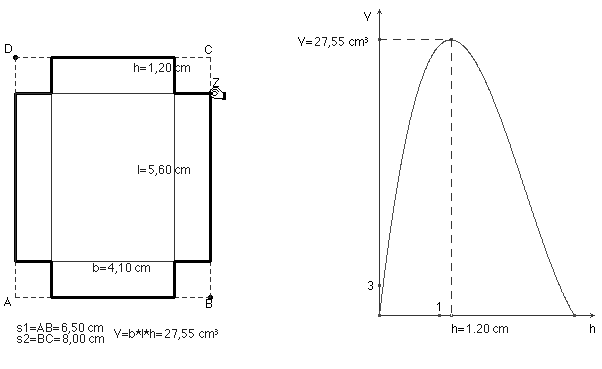
Abb. 9
Es ist also folgende Berechnungsaufgabe (exakt) zu lösen: Welche Abmessung für h erzielt das größte Schachtelvolumen, wenn das Verpackungsrechteck die Abmessungen s1 = 6,50 cm und s2 = 8,00 cm hat.
Dazu ist die zu maximierende Zielfunktion aufzustellen: Es ergibt sich eine kubische Funktionsgleichung: V(h) = (6,5 - 2 h) (8 - 2 h) h× . Dazu legen wir eine horizontale Sekante durch die Kurve für h ® V(h); es gilt: V(h + d) – V(h - d) = 0 (Abb. 10a).
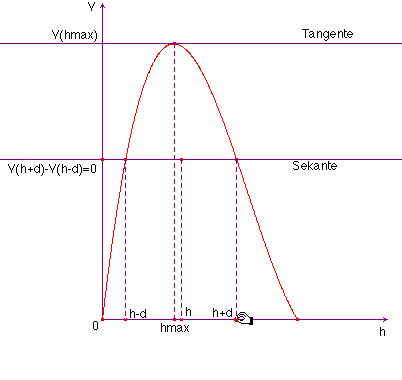 Abb. 10 a
Abb. 10 a
Wird d immer kleiner gemacht, so nähert sich die horizontale Sekante der horizontalen Tangente durch den maximalen Punkt an (Abb. 10 b) und der Mittelpunkt der entsprechenden Sehne läuft gegen den Extremalpunkt Abb. 10 c), d.h. in der vereinfachten Gleichung V(h + d) – V(h - d) = 0 ist d=0 zu setzen, um eine Bestimmungsgleichung für hmax zu gewinnen (vgl. die Zeilen 7-11 des Ausdrucks 1).
Im folgenden führen wir die Berechnung von hmax ,V(hmax) und den anderen Größen gänzlich mit Derive durch. Dazu werden nur folgende Optionen von Derive benötigt:
Vereinfachen, Faktorisieren, Substituieren, Lösen, Approximieren; zur Selbstkorrektur: Löschen; außerdem muß die Bedeutung des setzenden Gleichheitszeichen ("f(x):=") verstanden sein und das elementare Arbeiten mit dem Zeileneditor.
 | 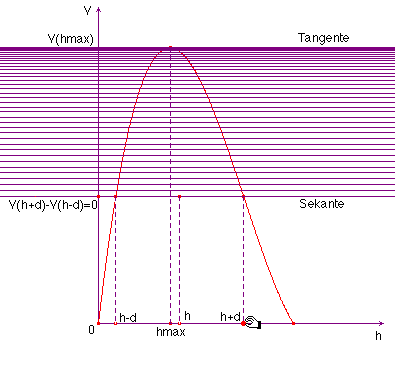 |
| Abb. 10 b | Abb 10 c |
Den dokumentierten Lösungsweg zeigt der Ausdruck 1. (Um Schreibarbeit zu sparen, wird statt hmax hm geschrieben.)
(Die komplizierte Lösung einer solchen Aufgabe mittels der Ungleichung vom arithmetischen und geometrischen Mittel ist in Natanson (1966) ausgeführt.)

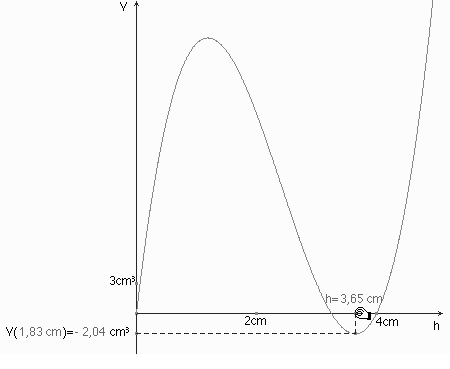 Abb. 11
Abb. 11
Die computergeometrisch ermittelten Näherungswerte können zu Kontrolle der approximierten Computeralgebraergebnisse dienen. Der Extremwert in Zeile 21 ist ein Minimumwert, das kann dem Schaubild von h ® V(h) bei erweitertem Definitionsbereich abgelesen werden. (Abb. 11) -Die Bestimmungsgleichung liefert eben alle Stellen, an denen eine horizontale Tangente existiert.
Für die entsprechende allgemeine Extremwertaufgabe erhält man mit Derive:
hmax = ![]() ; daraus ergibt sich sofort die Lösbarkeitsbedingung: s1>o,s2>o, wie zu erwarten war.
; daraus ergibt sich sofort die Lösbarkeitsbedingung: s1>o,s2>o, wie zu erwarten war.
(Die Schellbach-Methode hat bereits Appel (1993), wenn auch implizit, auf das vorstehende Beispiel angewendet; sie wird auch im bayerischen Unterrichtswerk "Mathematik an Realschulen" (Habler, E. et al. 1982) benutzt. Bereits im preußischen Unterrichtswerk "Die Mathematik auf den Gymnasien und Realschulen" von H. Müller (1899) wird diese Methode zur Lösung von Extremwertaufgaben beschrieben und angewendet.)
Beispiel 2 (Oberfläche eines Zylinders bei gegebenem Volumen)
Die Aufgabenstellung, die auf den experimentellen Nachweis der Existenz eines Extremums führen soll, zeigt ein interaktives Arbeitsblatt (Abb. 12)
Das zugehörige Schaubild läßt für ein Volumen von 100 cm³ ein Oberflächenminimum von etwa 119,27cm2 bei r » 2,5 cm erkennen (Abb. 13)
Auch die Variation vorgegebenen Volumens bestätigt die Existenz eines Minimums (Abb. 14). Es kann deshalb folgende allgemeine Extremwertaufgabe formuliert werden:
Berechne für einen Kreiszylinder vorgegebenen Volumens die minimale Oberfläche, den dazugehörigen Grundkreisradius und die Höhe.
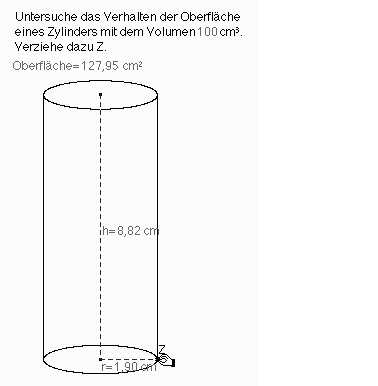
Abb. 12
Die Zielfunktion ist gebrochen rational. Der Lösungsweg mittels Derive ist im Ausdruck 2 dokumentiert. Die allgemeine Lösung wird zum Schluß für V0 = 100 cm³ spezifiziert.
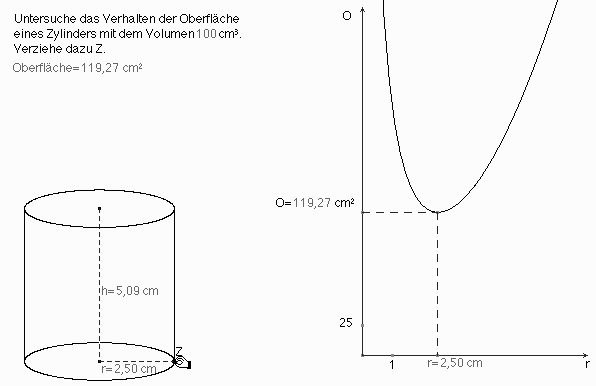
 Abb. 13
Abb. 13
Abb. 14
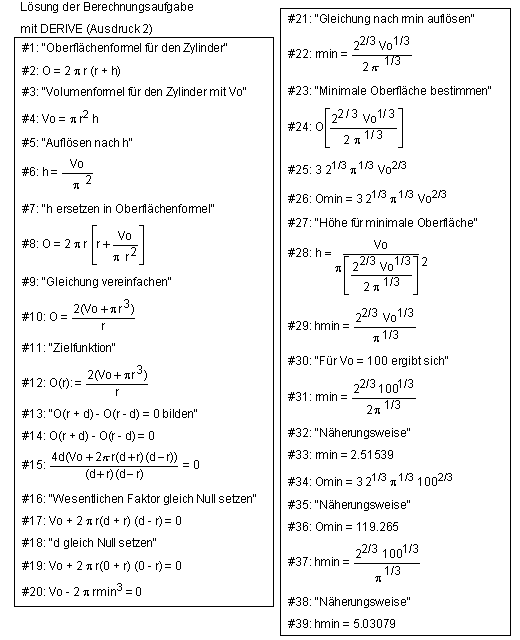
Bemerkung 1: Während die experimentelle Methode zur Entdeckung und zur näherungsweisen Lösung von Extremwertaufgaben mittels dynamischer Computergeometrie das Arbeiten in der Art des Trial and Error begünstigt, muß beim Einsatz von Computeralgebra zur exakten Lösung einer (allgemeinen) Extremwertaufgabe systematisch und planerisch vorgegangen werden. Beide Arbeitsstile ergänzen sich.
- Im wesentlichen kann die computerunterstützte Gesamtbehandlung von Extremwertaufgaben auch mit dem portablen Grafikcomputer TI - 92, in dem Derive und Cabri Géomètre II fest implementiert sind, realisiert werden. In der Hand des Lehrers/ der Lehrerin eignet sich der TI - 92 zusammen mit einem Datendisplay für den Tageslichtprojektor auch als Demonstrationsmedium.
Bemerkung 2: Die Behandlung von Extremwertaufgaben mit dynamischer Computergeometrie ist bereits ab Klasse 7 möglich, da die Gleichung bzw. der Term der Zielfunktion nicht explizit aufgestellt werden muß. Ab Klasse 9 erlaubt dann der mathematische Kenntnisstand die Einführung und Anwendung der Differenzmethode mit oder ohne Unterstützung durch Computeralgebra.
Bemerkung 3: Die computeralgebraische Lösung der Extremwertaufgaben als Berechnungsaufgaben versteht sich als Beitrag zur generellen Integration der Computeralgebra in den Mathematikunterricht der Sekundarstufe I.
|
Appel, H. (1993): |
Anwenden und Üben von Lerninhalten mit Hilfe des Programmes DERIVE. In: Computer und Unterricht, Heft 9, S. 57-61 |
||
|
Dörr, R. (1989): |
Extremwertaufgaben erst ab Klasse 11? In: Mathematik in der Schule (27), Heft 10, S. 688-698 |
||
|
Glatfeld, M. (1989): |
Bemerkungen zur Extremwertbestimmung kubischer Funktionen. In: Praxis der Mathematik (26) 1984, Heft 9, S. 267-270 |
||
|
Fermat, P. (1629)
Glatfeld, M. (1989): |
Abhandlungen über Maxima und Minima. Aus dem Lateinischen von Max Miller. Ostwalds Klassiker der Exakten Wissenschaften.- Leipzig: Akademische Verlagsgesellschaft 1934 Bemerkungen zum Thema "Extremwerte" in den Klassenstufen 9 und 10. In: mathematik lehren, Heft 37 (Dezember1989), S. 19-22 |
||
|
Habler, E. et al. (1982): |
Mathematik für Realschulen. MR10, Gruppe 1. Frankfurt am Main: Diesterweg, S. 178 |
||
|
Heugl, H. (1996): |
Mathematikunterricht mit Computeralgebra-Systemen. Bonn: Addison-Wesley |
||
|
Kutzler, B. (1995): |
Matehmatik unterrichten mit DERIVE. Bonn: Addison-Wesley |
||
|
Laborde, J.-M.; Bellmain, F. (1996): Müller, H. (1899) |
Cabri Géomètre II. Version 1.0 - Dallas/USA u. Freising: Texas Instruments. (Deutsche Oberfläche und Bearbeitung des Handbuchs von H. Schumann) Die Mathematik auf den Gymnasien und Realschulen, A II, Oberstufe. -Leipzig: Teubner |
Mathematik für Realschulen. MR10, Gruppe 1. Frankfurt am Main: Diesterweg, S. 178 |
|
|
Natanson, I. P. (1966): |
Einfachste Maxima- und Minima-Aufgaben. Berlin: Deutscher Verlag der Wissenschaften, S. 27/28 |
||
|
Rüthing, D. (1998):
Schönbeck, J.; Schupp, H. (Hg.) (1978): |
Computerunterstütztes Experimentieren und erklärendes Theoretisieren anhand eines komplexen Extremwertproblems. In: Mathematik in der Schule (36), Heft 11, S. 615-630 Mathematisches Unterrichtswerk PLUS, 9.Schuljahr. - Paderborn: Schöningh |
||
|
Schellbach, K.H. (1860) Schulz, M. (1989): |
Mathematische Lehrstunden. Aufgaben aus der Lehre vom Größten und Kleinsten.- Berlin: Georg Reimer Einige Gedanken zur gegenwärtigen und künftigen Behandlung von Extremwertaufgaben. In: Mathematik in der Schule (27), Heft 11, S. 745-753 |
||
|
Schumann, H. (1991): |
Experimentelles Lösen einfacher isoperimetrischer Probleme in einer interaktiven computergrafischen Lernumgebung. In: Didaktik der Mathematik (19), Heft 3, S. 227-241 |
||
|
Schumann, H. (1992): |
Schulgeometrisches Konstruieren mit dem Computer. -Stuttgart: Metzler u. Teubner |
||
|
Schumann, H. (1997): |
Neue Standards für das Lösen geometrischer Berechnungsaufgaben durch Computernutzung. In: MNU. Der mathematische und naturwissenschaftliche Unterricht (50), Heft 3, S. 172-175 |
||
|
Schumann, H. (1998): |
Dynamische Behandlung elementarer Funktionen In: Mathematik in der Schule (36), Heft 3, S. 172-188 |
||
|
Schumann, H. (1998): |
Interaktive Arbeitsblätter für das Geometrielernen. In: Mathematik in der Schule (36), Heft 10, S. 562-569 |
||
|
Schumann, H. (1998): |
Geometrische Extremwertaufgaben in dynamischer Behandlung. In: Zentralblatt für Didaktik der Mathematik (30),Nummer 6, S. 215-223 |
||
|
Schupp, H. (Hg.) (1997): |
Optimieren. Themenheft mathematik lehren Nr. 81 (April 1997) |
||