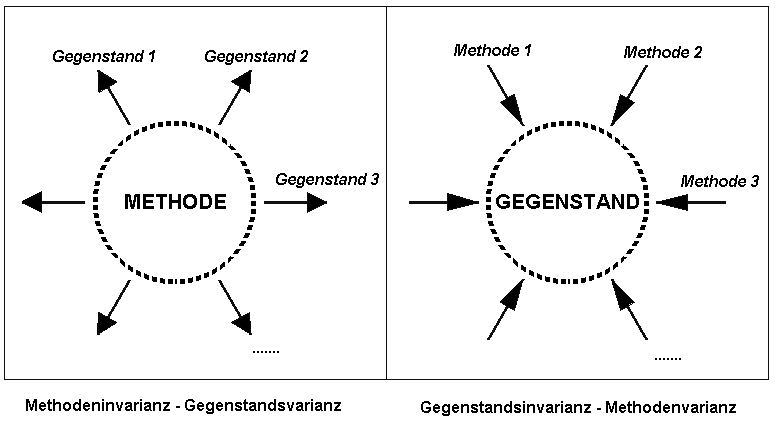
 Diagramm 1
Diagramm 1Methodenvariation mittels Dynamischer Geometrie am Beispiel umfangs- und flächengleicher Rechtecke
| Um eine Sache vollständig zu verstehen, muss man sie auf verschiedene Weise verstanden haben. |
| Frei nach R.Freynman (1918 - 1988) |
Kurzreferat: Die Ursachen für die Dominanz der Methodendemonstration an verschiedenen mathematischen bzw. mathematisierbaren Gegenständen über die Gegenstandsexploration mittels verschiedener Methoden sind curricularer Natur. Eine Balance zwischen diesen beiden Grundmustern des Mathematikunterrichts kann durch die Anwendung des Spiralprinzips und des Prinzips der computerunterstützten Methodenvariation erreicht werden. In der vorliegenden Arbeit wird das exemplarisch am Gegenstand "Umfangs- und flächengleiche Rechtecke" (Klassenstufe 5-10) mittels Dynamischer Geometrie konkretisiert. Die computer-generierte Phänomenologie erfährt eine Begründung auf schulalgebraischem Niveau. Die Arbeit schließt mit dem Hinweis auf notwendige thematische Erweiterungen und ungeklärte Schnittstellenprobleme bei der Anwendung verschiedener medienspezifischer Methoden.
1 Einleitung
Schupp (unter anderem 1996) hat mit Recht kritisiert, dass im üblichen Mathematik-unterricht Methoden eingeführt werden, um diese an dafür geeigneten Gegen-ständen zu demonstrieren – anstelle Gegenstände mittels mehrerer geeigneter Methoden zu explorieren (Diagramm 1). Die Ursachen für das Primat der Methodensystematik dürften in der Linearität des schulischen Curriculums, in dem die mathematischen Werkzeuge hierarchisch von Klassenstufe zu Klassenstufe entwickelt werden, und in der leichteren Lehrbarkeit und Lernbarkeit zu suchen sein.
Es wäre schon viel gewonnen, wenn eine Balance zwischen Methodenuniformität bei Gegenstandsvariation und Methodenvariation bei Gegenstandsexploration im Mathematikunterricht erreicht werden könnte. Vehikel zur Ausbalancierung sind erstens das Spiralprinzip mit seiner Ausprägung als Prinzip des vorwegnehmenden Lernens: "Die Behandlung eines Wissensgebietes soll nicht aufgeschoben werden, bis eine endgültig-abschließende Behandlung möglich erscheint, sondern ist bereits auf früheren Stufen in einfacher Form einzuleiten." sowie mit seiner Ausprägung als
 Diagramm 1
Diagramm 1
Prinzip der Fortsetzbarkeit: "Die Auswahl und die Behandlung eines Themas an einer bestimmten Stelle des Curriculums soll nicht ad hoc, sondern so erfolgen, daß auf höherem Niveau ein Ausbau möglich wird..." (Wittmann 1981) und zweitens das Prinzip der "computerunterstützten Methodenvariation": Mathematische Werkzeugssoftware eröffnet vielfältige Möglichkeiten der Exploration mathematischer Unterrichtsgegenstände bei der die Verwendung von Optionen mit Black-Box-Charakter ein "vorwegnehmendes Lernen" erleichtert. Die Gefahr der Nutzung solcher Optionen, liegt aber im Stehenbleiben bei den computergenerierten experimentellen Phänomenen. Es sollte stets auch die Begründung für die Phänomene erarbeitet werden, und das geht eben meist nur ohne die Nutzung von Computerwerkzeugen.
Die Wahl des Gegenstandes: "Umfangs- und flächengleiche Rechtecks" (Klasse 5-10) wird deshalb getroffen, weil es sich um ein sehr beziehungshaltiges und anwendungsträchtiges Thema handelt, an dem operatives und funktionales Denken sowie die intellektuellen Techniken des Abstrahierens und Analogisierens geübt werden können, und weil sowohl die Schüler und Schülerinnen als auch die Erwachsenen ihre Schwierigkeiten mit der Isoperimetrie haben.
Da es um ein geometrisches Thema geht, liegt es auf der Hand, ein Dynamisches Geometriesystem (DGS) zu verwenden; es soll auf exemplarische Weise verdeutlicht werden, wie ausdrucksreich die computerunterstützte Methodenvariation durch direkt-manipulative Dynamisierung von Figuren sein kann. Als DGS wurde Cabri Géomètre II (Laborde et al. 1996) gewählt, weil es über notwendige Optionen verfügt, die andere Systeme nicht besitzen.
Welche kognitiven Lernziele (Grobzielformat) sind u. a. bei diesem Thema zu verfolgen:
Die Schüler sollen wissen und verstehen, dass
Zur Gegenstandsexploration werden den Schülern und Schülerinnen interaktive Arbeitsblätter (Schumann 1998a) zur Verfügung gestellt, die als Versuchsanordnungen fungieren. Jedes der Arbeitsblätter verkörpert eine Methode. Eine breite induktive Basis für die Abstraktion zur Theorieebene hin ist durch die direkt-manipulative Variation der vorgegebenen Figuren und der vorgegebenen Maß-zahlen gewährleistet. Von der Anwendung der experimentellen Methoden der dynamischen Geometrie wird von Klassenstufe 7/8 an zu schulalgebraischen Begründungs- bzw. Erklärungsmethoden übergegangen. – Die Konformität mit dem mathematischen Kerncurriculum bleibt weitgehend gewahrt.
2.1 Klassenstufe 5/6
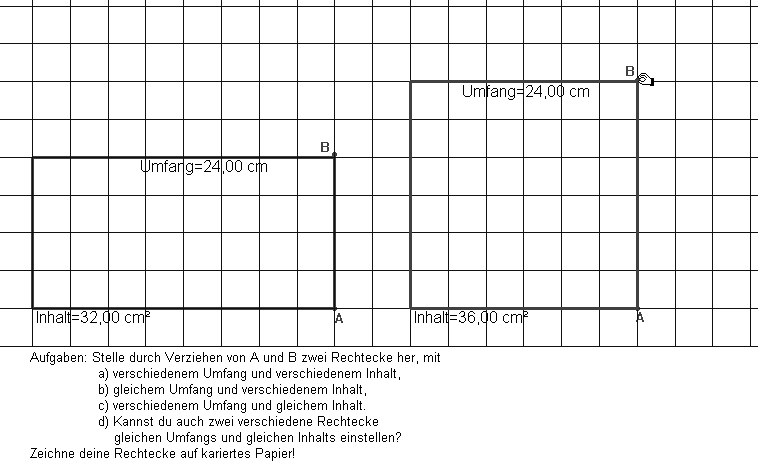
Die zu bearbeitenden Arbeitsblätter dienen der ersten Berührung mit dem Thema. Das Verziehen der Punkte A und B (Abb.1 -eine offene Aufgabenstellung) geschieht im Punktfang. (Im Gitter gibt es natürlich bei umfangsgleichen Rechtecken nur für eine durch vier teilbare Umfangsmaßzahl und bei fächengleichen Rechtecken nur für eine Fächenmaßzahl, die eine Quadratzahl ist, ein optimales quadratisches Rechteck.) Die Versuchsanordnung in Abbildung 2.1 ist so konstruiert, dass die Rechtecke umfangsgleich bleiben. Erkenntnis: das quadratische Rechteck hat größten Inhalt (Abb. 2.2; die Anzahl der verschiedenen umfangsgleiche Rechtecke ergibt sich generell aus den additiven Zerlegungen des halben Umfangs in zwei Summanden). – Die Schüler und Schülerinnen haben erfahrungsgemäß mehr Schwierigkeiten einzusehen, dass umfangsgleiche Rechtecke unerschiedlichen Inhalt haben können als flächengleiche Rechtecke unterschiedlichen Umfang:
 So konnten von 125 Schülern/Schülerinnen der Klassenstufe 6 (Realschule) nur ca. 20% zwei verschiedene umfangsgleiche Rechtecke unterschiedlichen Inhalts aber immerhin ca. doppelt so viele zwei verschiedene inhaltsgleiche Rechtecke unterschiedlichen Umfangs in ein quadratisches Gitter einzeichnen.
So konnten von 125 Schülern/Schülerinnen der Klassenstufe 6 (Realschule) nur ca. 20% zwei verschiedene umfangsgleiche Rechtecke unterschiedlichen Inhalts aber immerhin ca. doppelt so viele zwei verschiedene inhaltsgleiche Rechtecke unterschiedlichen Umfangs in ein quadratisches Gitter einzeichnen.
Abb.1
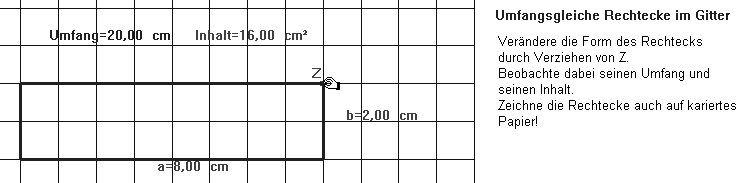
Abb. 2.1
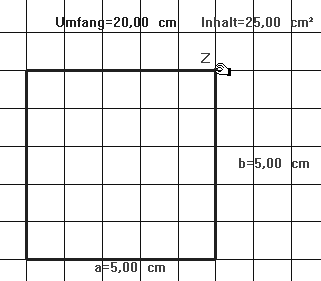 Abb. 2.2
Abb. 2.2
Das Arbeitsblatt in Abbildung 3.1 dient der Erkenntnisfindung, dass sich die Einheitsquadrate zu flächengleichen Rechtecken verschiedener Form zusammensetzen lassen, die verschieden großen Umfang besitzen (Abb. 3.2: die Lösungen ergeben sich generell aus den multiplikativen Zerlegungen der Zahl der Einheitsquadrate in zwei Faktoren).
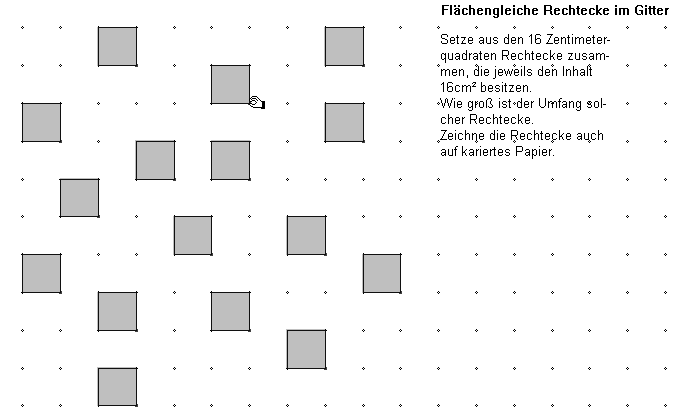
Abb. 3.1
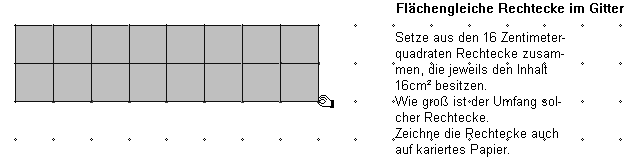
Abb. 3.2
– In Klasse 6 können dann einfache Dezimalzahlen als Maßzahlen verwendet werden. Eine entsprechend segmentierte Umfangsstrecke wird aufgefaltet zu einem Rechteck ABCD (Abb. 4.1/2). Durch Variation des Teilpunktes D wird das Verhältnis der Seiten variiert und dabei herausgefunden, dass der Inhalt immer größer wird, wenn man den Seitenunterschied kleiner macht; er wird am größten, wenn das Rechteck quadratisch ist (Abb. 4.2/3).
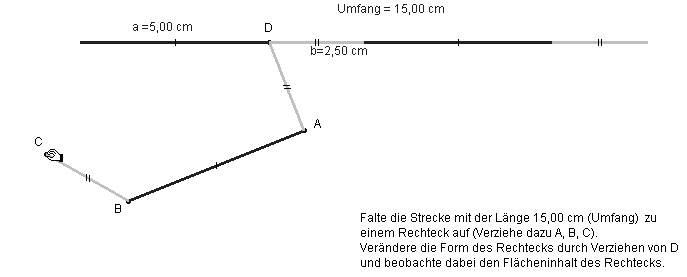
Abb. 4.1
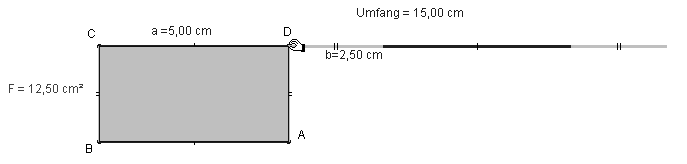
Abb. 4.2
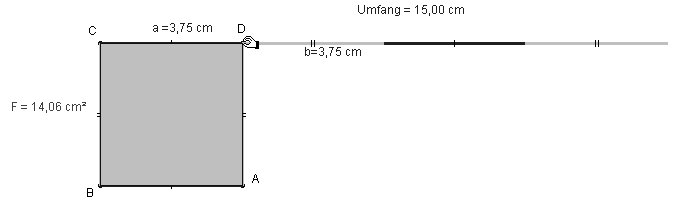
Abb. 4.3
2.2 Klassenstufe 7/8
Während in Klasse 5/6 im wesentlichen nur die experimentelle Erkenntnisfindung im Vordergrund steht, können in der Klassenstufe 7/8 mit den dann zur Verfügung stehenden schulalgebraischen Werkzeugen Erkenntnisbegründungen vorgenommen werden. Dabei muss von den konkreten Größen zu den Variablen für Größen abstrahiert werden. Die Methoden für die systematische Konstruktion umfangs- bzw. flächengleicher Rechtecke treten verstärkt hinzu: Wie gewinnt man aus einem Rechteck ein umfangsgleiches, das größeren (kleineren) Inhalt hat, und wie lässt sich diese Verwandlung mit einer geometrischen Konstruktion bewerkstelligen?
Die Folge der Abbildungen 5.1-5.7 zeigt einen solchen gegenständlichen umfangsgleichen Verwandlungsprozess (Schumann 1985), wobei durch nachträgliche Variation des abzuschneidenden Stücks, die maximale Flächenvergrößerung sich als quadratische herausstellt und das entstehende Rechteck ebenfalls quadratisch ist (Abb. 5.8). Die entsprechende herkömmliche Konstruktion mit Zirkel und Lineal oder mit dem Geo-Dreieck (dann muss aber gemessen werden!) ist recht einfach.
Hier bietet es sich nun an von der bildhaften Darstellung zur fomalsprachlichen Beschreibung überzugehen:
Sei die Rechtecklänge a, die Rechteckbreite b und c die Verkürzung der Recht-ecklänge, so ist der Flächengewinn [a - (b + c)] c = (a - b) c - c2, der am größten wird für c = (a - b) / 2: maximaler Wert ((a - b) / 2)2. Das flächengrößte Rechteck hat dann die Seitenlängen a - (a - b) / 2 und b + (a - b) / 2 und diese sind gleich dem arithmetischen Mittel von a und b: (a + b) / 2. Die Umkehrung des Verwandlungsprozesses liefert ein umfanggleiches, aber flächenkleineres Rechteck.
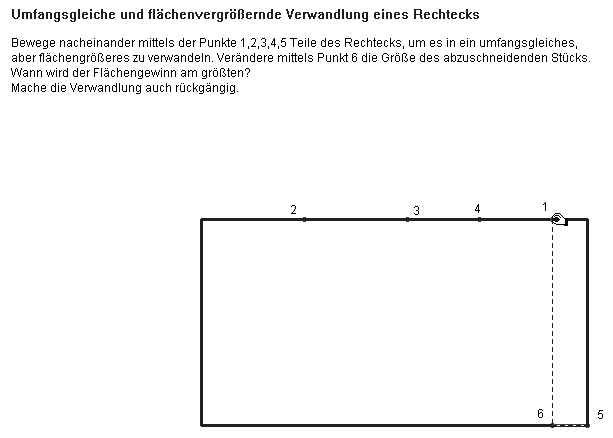 Abb. 5.1
Abb. 5.1
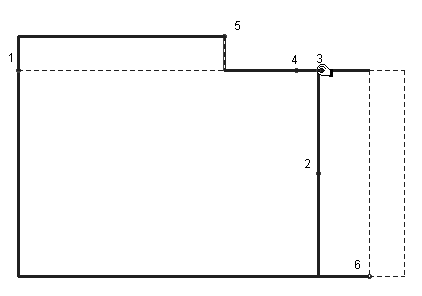
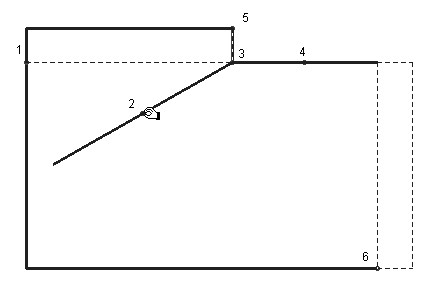
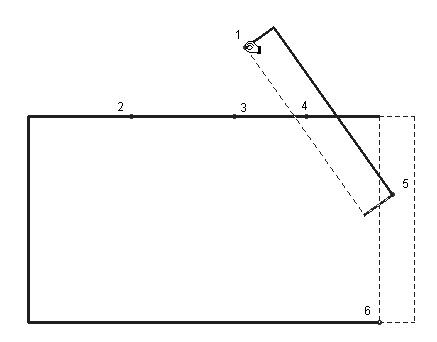
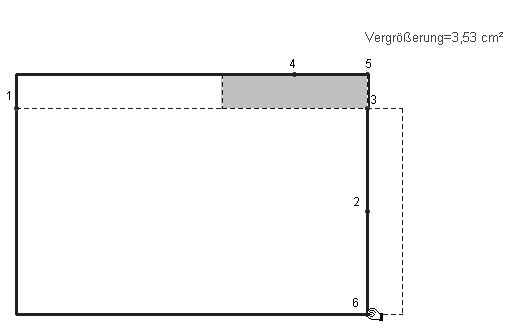
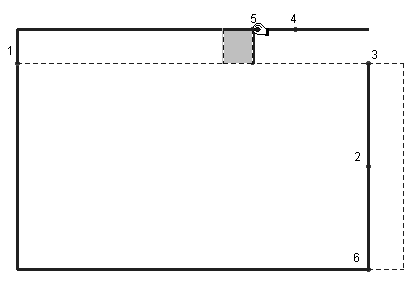

Abb. 5.2 - 5.7
Abb. 5.8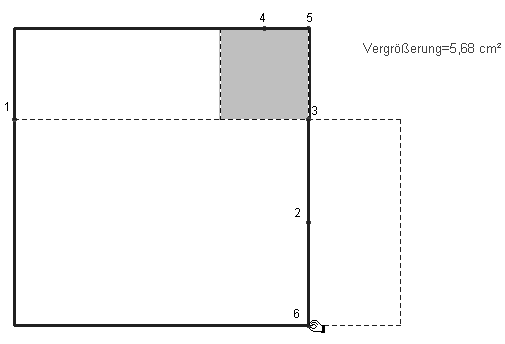
Bei der umfangsgleichen und flächenvergrößernden Rechteckverwandlung muss ein Ausgleich der Seitenlängen stattfinden, damit der Umfang invariant bleibt (Abb. 6). Um wieviel wird der Inhalt größer? – Mit |AB| = a, |BC| = b, a > b und a‘ = a – c ,
b‘ = b + c (nach Konstruktion) ist ab < a’b‘ = (a - c) (b + c) gleichwertig mit
0 < (a - b) c - c2 (Flächengewinn) und das ist genau dann der Fall, wenn c < a - b. – Geht man vom Rechteck A’B’C’D‘ zum umfangsgleichen Rechteck ABCD über, so ergibt sich ein Flächenverlust, der mit a‘ und b‘ auszudrücken ist (Umrechnung des Flächengewinns!).
Wie gewinnt man aus einem Rechteck ein flächengleiches mit unterschiedlichem Umfang?
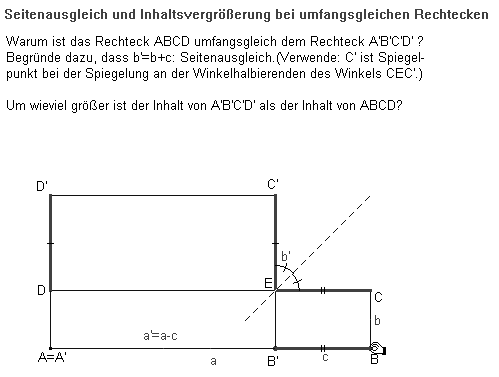
Abb. 6
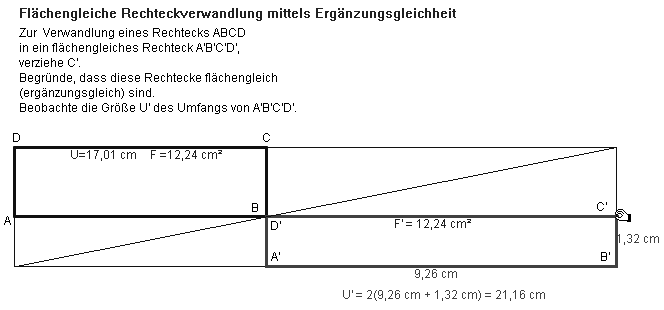 Abb. 7.1
Abb. 7.1
Mittels ergänzungsgleicher Rechtecke lässt sich eine solche Verwandlung leicht herstellen (Abb. 7.1). Eine entsprechende Zirkel-Lineal-Konstruktion oder eine Konstruktion mit dem Geo-Dreieck ist nicht schwierig. Das variierbare Rechteck hat minimalen Umfang, wenn es quadratisch wird (Abb. 7.2).
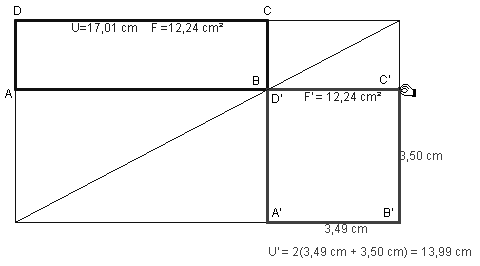 Abb. 7.2
Abb. 7.2
Bei der flächengleichen und umfangsverkleinernden Rechteckverwandlung muss ein Ausgleich der Flächengröße stattfinden, damit der Inhalt invariant bleibt (Abb. 8). Um wieviel wird der Umfang kleiner? – Mit |AB| = a, |BC| = b, a > b und a‘ = a - c1,
b‘ = b + c2 ist ab = a’b‘ (nach Konstruktion). Die Rechtecke haben als Fläche gemeinsam das Rechteck AB’ED; aus ab = (a - c1) (b + c2) ergibt sich:
c2 = c1 b / (a - c1) und U > U‘ ist gleichwertig mit (c12 - (a - b) c1) / (a - c1) < 0 (Umfangsverlust: ((a - b) c1 – c12) / (a – c1) und das ist genau dann der Fall, wenn
c1 < a – b. Geht man vom Rechteck A’B’C’D‘ zum flächengleichen Rechteck über, so ergibt sich ein Umfangsgewinn, der mit a‘ und b‘ auszudrücken ist (Umrechnung des Umfangsverlustes!).
Mit der Identität (a + b)2 = 4ab + (a – b)2 können nun die optimalen Rechteckeigenschaften des Quadrats begründet werden: Wenn der Umfang der Rechtecke mit den Seitenlängen a, b konstant ist, so auch (a + b) 2 : der Summand
4ab und damit der Inhalt wird am größten, wenn (a - b) 2 = 0, als wenn a = b (Abb. 9). Außerdem liest man ab, dass der Inhalt größer (kleiner) wird, wenn der Seitenunterschied kleiner (größer) wird. Wenn der Flächeninhalt konstant ist, so auch 4ab. Die Summe (U/2) 2 = 4ab + (a - b) 2 wird am kleinsten, also der Umfang wird minimal, wenn (a - b)2 = 0, d.h., wenn a = b (Abb. 10). Der Umfang wird kleiner (größer), wenn der Seitenunterschied kleiner (größer) wird.
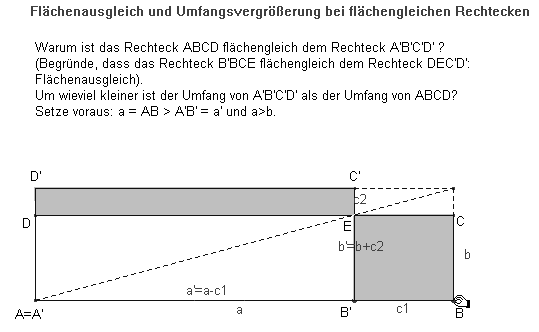 Abb. 8
Abb. 8
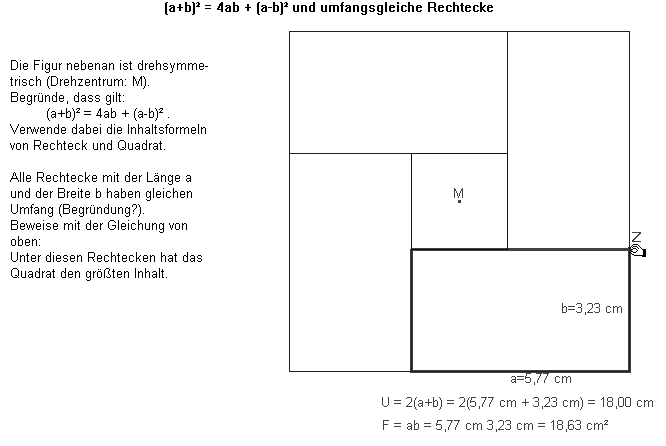
Abb. 9
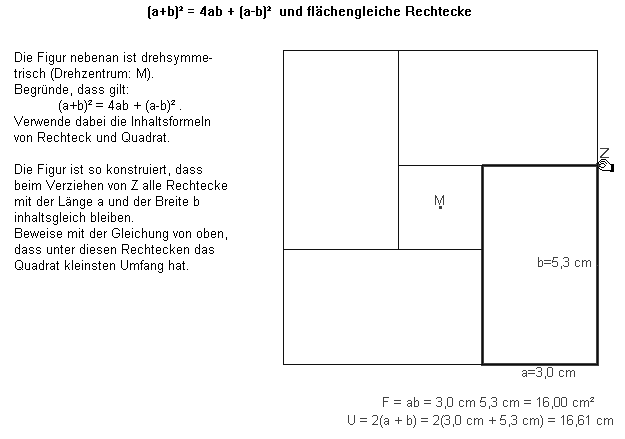 Abb. 10
Abb. 10
Wir beziehen nun die funktionale Betrachtungsweise explizit ein, indem wir die funktionalen Abhängigkeit der Seitenlängen voneinander bei umfangsgleichen (flächengleichen) Rechtecken untersuchen. Dabei gehen wir von der Erzeugung eines "figurengebundenen" Schaubildes aus. Bei umfangsgleichen Rechtecken erzeugt die freie Ecke eine Spur (Abb. 11.1), die Ecke bewegt sich auf einer referenzierbaren Ortslinie, die von einer Geraden (Abb. 11.2) der Funktionsgleichung
b = U0 / 2 – a getragen wird usw. Bei flächengleichen Rechtecken erzeugt, die freie Ecke den Ast der rechtwinkligen Hyperbel im ersten Quadranten (Abb. 12) mit der Funktionsgleichung b = F0/a usw.
Rechtecke mit vorgegebenem Umfang und Inhalt können im Arbeitsblatt der Abbildung 13.1 eingestellt werden. Der experimentell bestimmte Eckpunkt fällt mit dem Schnittpunkt der entsprechenden Ortslinien zusammen (Abb 13.2); die zweite Lösung ist spiegelsymmetrisch zur ersten. In Klasse 9 ergibt sich dann die exakte arithmetische/algebraische Lösung mit der üblichen quadratischen Gleichung.
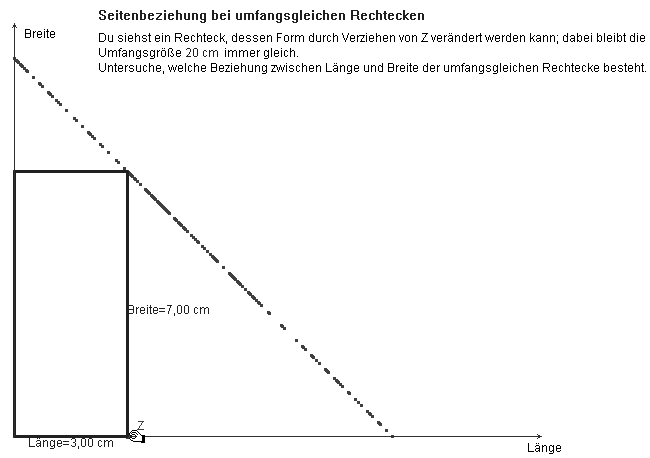 Abb. 11.1
Abb. 11.1
 Abb. 11.2
Abb. 11.2
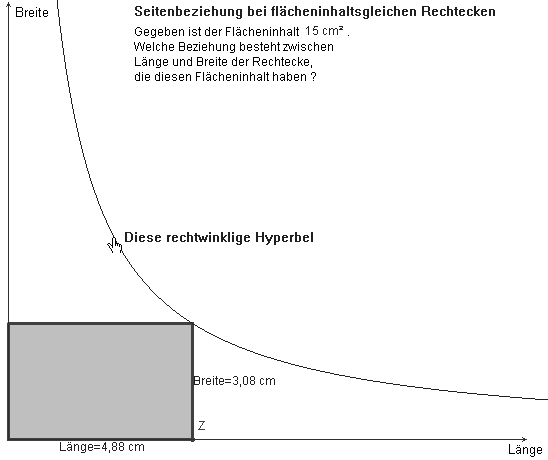 Abb. 12
Abb. 12

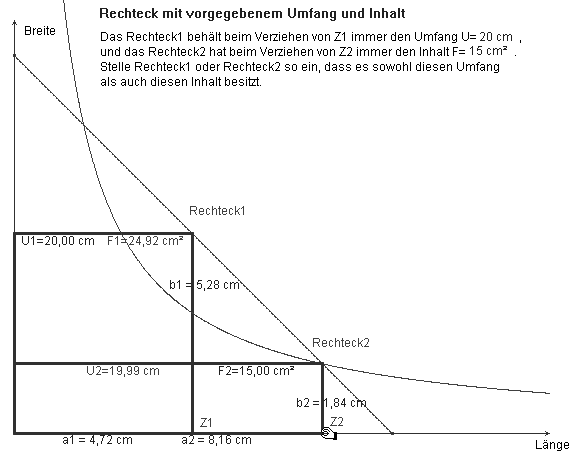
Abb. 13.1/2
2.3 Klassenstufe 9/10
Wir setzen die in Klasse 8 begonnene funktionale Betrachtungsweise fort, indem wir die funktionale Abhängigkeit des Inhalts (Umfangs) von einer der Seitenlängen umfangsgleicher (inhaltsgleicher) Rechtecke untersuchen. Dabei benutzen wir die Möglichkeit, Meßwerte, die von grafischen Figurenparametern abhängen, in Form von Schaubildern als Ortskurven ausgeben zu lassen. –Solche funktionale Beziehungen kann man "quasi-empirisch" nennen (Schumann 1998b); in der Black-Box für die Meßwerte sind natürlich die entsprechenden Berechnungen versteckt.
In der Abbildung 14.1 wird der Flächeninhalt umfanggleicher Rechtecke in Abhängigkeit von der Rechtecklänge ausgegeben. Wir schalten in Abbildung 14.2 den 1. Quadranten eines Koordinationssystems ein, um die funktionale Abhängigkeit grafisch zu veranschaulichen – ohne den Funktionsterm zu kennen). Wie lautet der Funktionsterm explizit? Aus U0 = 2 (a + b) und F = ab folgt F = a(U0 / 2 - a). Es liegt
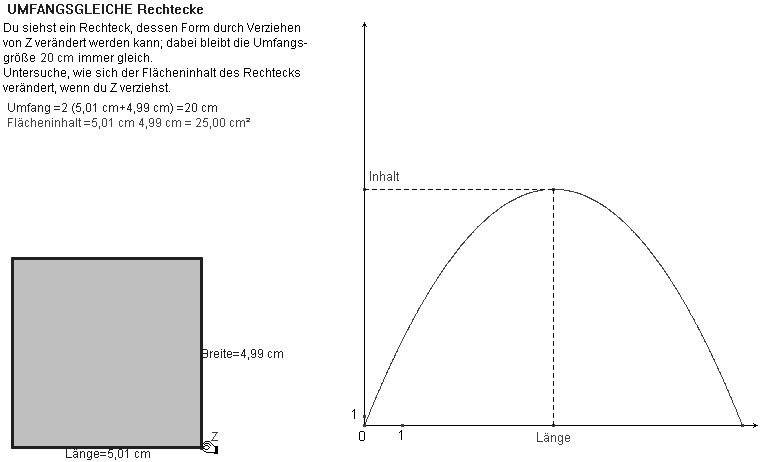 Abb. 14.1
Abb. 14.1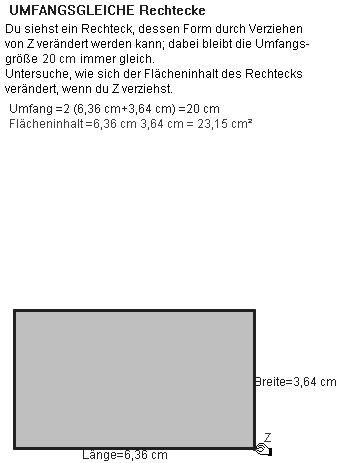
Abb.14.2
eine quadratische Funktion vor, deren Schaubild eine nach unten offen Parabel mit dem Scheitelpunkt (as; Fs) als maximalen Punkt ist. as ist das arithmetische Mittel der Nullstellen a= 0 und a = U0/2 : as = U0/4; Fs = (U0/4)2; das Rechteck mit maximalem Inhalt ist ein Quadrat der Seitenlänge U0/4.
Entsprechend ergibt sich bei flächengleichen Rechtecken (Abb. 15.1/2) für den Umfang in Abhängigkeit von einer der Rechteckseiten: U = 2 (a + F0 / a) (U ist das Doppelte der "Summe aus der Winkelhabierenden und einer quadratischen Hyperbel" im 1. Quadanten). Dem Schaubild und dem Funktionsterm liest man ab: Wenn a gegen Null geht oder gegen unendliche, so geht U gegen unendlich.
Extremwertbestimmung mittels quadratische Ergänzung:
U/2 = a + 2![]() + F0/a – 2
+ F0/a – 2![]() = (
= (![]() +
+![]() )2 - 2
)2 - 2![]()
U ist minimal, wenn der positive Minuend gleich null ist, also wenn ![]() +
+![]() = 0. Es ergibt sich a =
= 0. Es ergibt sich a =![]() für a >
0 und Umin = 4
für a >
0 und Umin = 4![]() ; das umfangsminimale Rechteck ist ein Quadrat der Seitenlänge
; das umfangsminimale Rechteck ist ein Quadrat der Seitenlänge ![]() .
.
Wir untersuchen nun, wie der Inhalt (Umfang) bei umfangsgleichen (inhaltsgleichen) Rechtecken vom Seitenunterschied (Betrag der Seitendifferenz) abhängt. Am Schaubild für den Inhalt in Abhängigkeit vom Seitenunterschied bei umfangsgleichen Rechtecken erkennen wir, wie der Inhalt abnimmt, wenn der Seitenunterschied zunimmt usw (Abb. 16). Es folgt aus U0 = 2 (a + b) und F = ab mit der schon in Klassenstufe 7/8 verwendeten Identität (a + b)2 = 4ab + (a - b)2:
F = (U0/4)2 - 1/4(a - b)2; das Schaubild im 1. Quadranten ist also die "Hälfte" einer nach unten offenen Parabel. F ist maximal, genau dann, wenn der Seitenunterschied gleich null ist, also, wenn a = b usw.
Am Schaubild für den Inhalt in Abhängigkeit vom Seitenunterschied bei inhaltsgleichen Rechtecken erkennt man, wie der Umfang zunimmt, wenn der Seitenunterschied zunimmt usw (Abb. 17). Es ergibt sich als Funktionsterm U = 2![]() ;
;
es liegt also eine Wurzelfunktion vor (Schaubild: halber Ast einer rechtwinkligen Hyperbel). Der Radikand ist am kleinsten, wenn der Seitenunterschied gleich null ist, also, wenn a = b = ![]() und Umin = 4
und Umin = 4![]() .
.
Wir kehren nun zu synthetisch-geometrischen Methoden zurück, indem wir die Beziehung flächengleicher Rechteckverwandlung mit der Ähnlichkeitslehre herstellen.

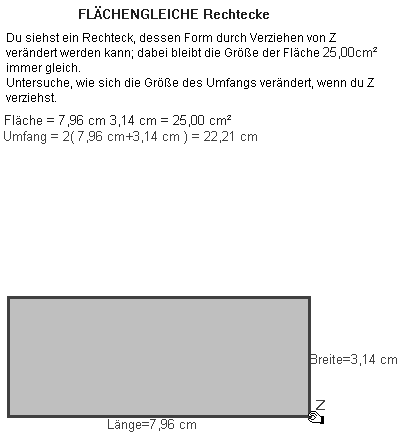 Abb. 15.1
Abb. 15.1
Abb. 15.2
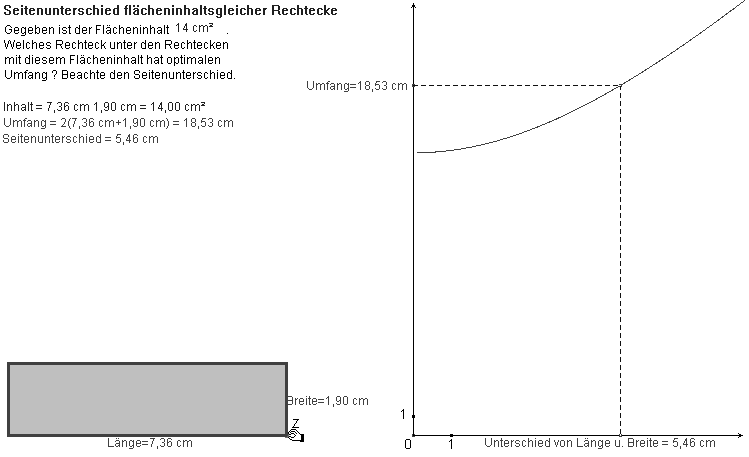
 Abb 16
Abb 16
Abb. 17
So kann man z.B. den 2. Strahlensatz verwenden, um ein Rechteck flächengleich zu verwandeln (Abb. 18; es gilt: a/a‘ = b‘/b).
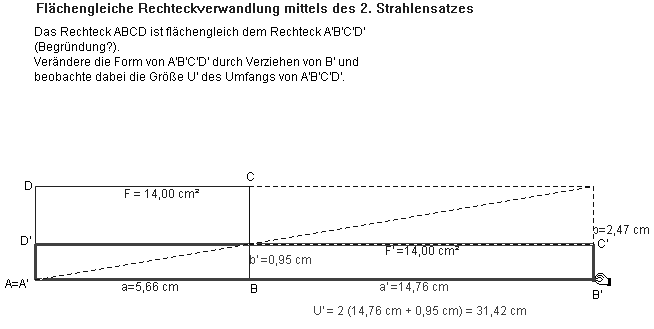 Abb. 18
Abb. 18
Die Abbildung 19.1 zeigt die flächengleiche Verwandlung von Rechtecken aus den Hypotenusenabschnitten nach dem Höhensatz (Danckwerts (1999) verwendet als Zugpunkt den Mittelpunkt des Thaleskreises). Der Umfang wird minimal, wenn der Höhenfußpunkt Z mit dem Thaleskreismittelpunkt zusammenfällt, d.h., wenn das Hypotenusenabschnittsrechteck zu einem dem Quadrat über der Höhe kongruenten Quadrat wird (Abb. 19.2). Begründung der experimentell gefundenen Erkenntnis:
Es ist U/2 = c = q + p ³ 2h, denn die Höhe h ist so groß wie die halbe Sehne zu der der Durchmesser AB Symmetrieachse. U wird minimal, wenn c = 2h, d.h., wenn das Dreieck ABC gleichschenklig ist, also wenn q = p ist. – Entsprechend kann auch die Höhensatz-Figur so konstruiert werden, dass mit ihr Rechtecke umfangsgleich verwandelt werden können.
Auch mittels des Kathetensatzes kann die flächengleiche Verwandlung flächengleicher Rechtecke vorgenommen werden (Abb. 20.1). Der Umfang wird minimal, wenn der Höhenfußpunkt Z mit A und C zusammenfällt (Abb. 20.2). Zur Begründung: Es ist U/2 = q + c ³ 2a. Mit a2 = c q folgt daraus (c - q)2 ³ 0. Das Gleichheitszeichen gilt genau dann, wenn c = q, also wenn das Rechteck aus Hypotenuse und Hypotenusenabschnitt in ein Quadrat übergeht, das kongruent zum Kathetenquadrat
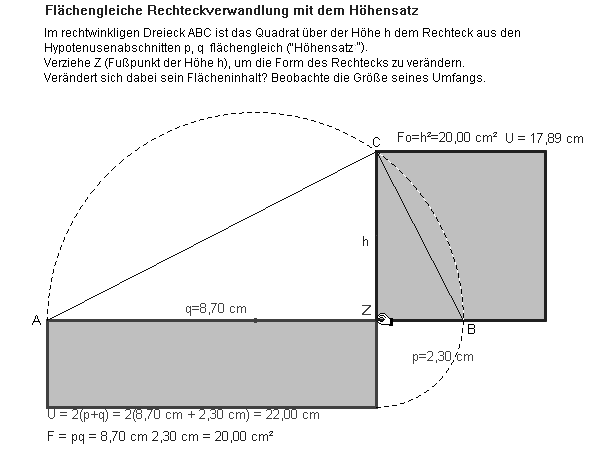
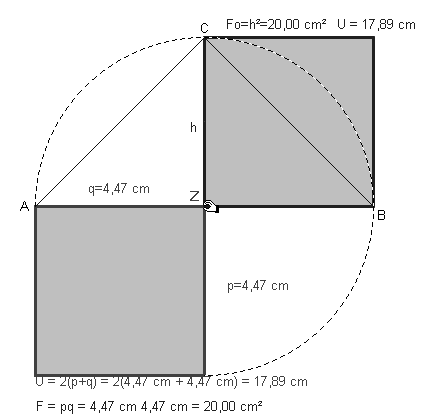 Abb. 19.1/2
Abb. 19.1/2
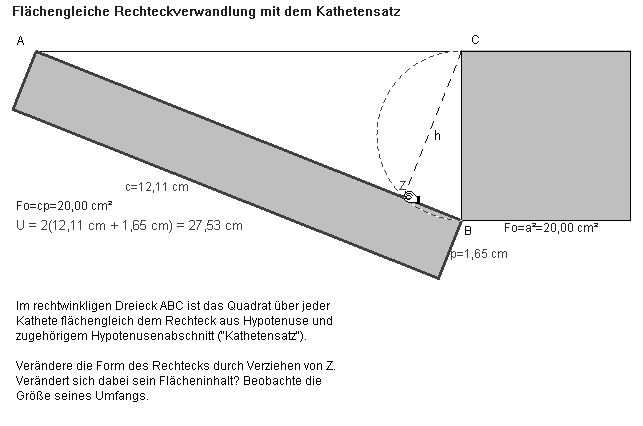 Abb. 20.1
Abb. 20.1
 Abb. 20.2
Abb. 20.2
ist. (Entsprechend lässt sich auch die Kathetensatz-Figur so konstruieren, dass mit ihr umfangsgleiche Rechteckverwandlungen durchführbar sind.)
Wir schließen die Methodenvariation mit dem flächengleichen Verwandeln durch Scherung (Abb. 21.1). Das Schaubild für die empirische Funktion ß ® U´´ ist in Abbildung 21.2 zu sehen. – Es ist F0 = a b = a´´ b´´ = (a/sin ß) (b sin ß) und
U´´ = 2(a´´ + b´´) = 2(F0 / (b sin ß) + b sin ß) für 0°<
ß £
90°. (Damit können wir bei der Behandlung unseres Themas mit Ausname der Exponential- und Logarithmus-funktion alle für die Sekundarstufe I relevanten Funktionstypen repräsentieren.) Die Extremwertbestimmung für den Umfang U´´ erfolgt wieder mittels quadratischer Ergänzung: Bedingung für das Minimum ist b sin ß = ![]() =
= ![]() , also gilt für den
, also gilt für den  extremalen Scherungswinkel ß = arcsin (
extremalen Scherungswinkel ß = arcsin (![]() ). Mit sin2 ß = a/b ergibt sich a´´= b´´.
). Mit sin2 ß = a/b ergibt sich a´´= b´´.
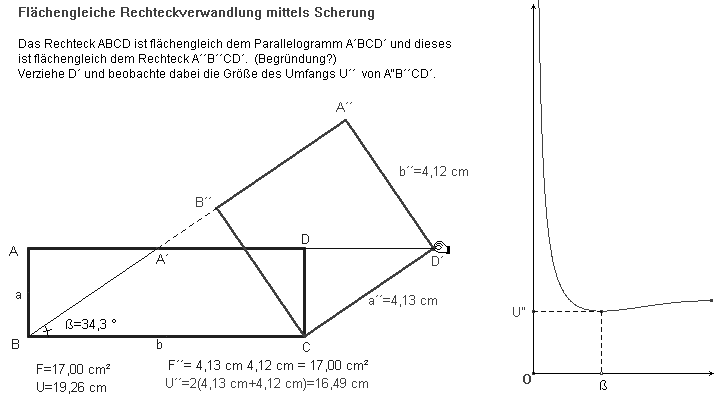
Abb. 21.1/2
3 Schlußbemerkungen
Die vorstehenden Methoden bilden nur eine Auswahl an Methoden für den Gegenstand "Umfangs- und flächengleiche Rechtecke". So wurden die Ungleichung vom arithmetischen und geometrischen Mittel und approximative Verfahren der flächen-gleichen Verwandlung eines Rechtecks in das Quadrat (z.B. nach Heron) nicht ein-bezogen. Die Verwendung der genannten Mittelungleichung für unseren Unterrichts-gegenstand erachten wir aber als weniger geeignet für die Sekundarstufe I. Natürlich fehlt die generalisierende Behandlung des Themas für allgemeinere Figuren als Rechtecke und die räumliche Analogisierung z.B. zum Quader (Kantensumme, Oberfläche und Volumen), wozu ensprechend 3D-Werkzeuge heranzuziehen wären.
Neben den computerorientierten Methoden für die Geometrie (Diagramm 2), etwa den Methoden der Dynamischen Geometrie, treten die traditionellen Papier- und Bleistift-Methoden (z.B. die geometrischen Konstruktionsmethode mit den Analog-werkzeugen Zirkel und Lineal) sowie die materialen Methoden (materiale Konstruk-tionsmethoden oder Methoden anhand materialer Modelle, z.B. eine geknüpfte Schnur als konstanter Umfang). Wir sind hier nur teilweise auf das mögliche Zusammenspiel dieser unterschiedlichen medienorientierten bzw. medienspezifi-schen Methoden eingegangen, um den Rahmen dieser Arbeit nicht zu sprengen. Für derartige Schnittstellenprobleme gibt es wohl keine endgültigen Lösungen; auch
fehlen noch entsprechende unterrichtspraktische Evaluationsergebnisse.
 Diagramm 2
Diagramm 2
Auf ähnliche Weise wie die hier durchgeführte Methodenvariation könnten auch andere Unterrichtsgegenstände für computerisierte Lernumgebungen aufbereitet werden. In diesem Sinne versteht sich diese exemplarische Arbeit als Diskussions-beitrag zur Entwicklung eines computerintegrierenden Curriculums für den Mathe-matikunterricht in der Sekundarstufe I.
4 Literatur
Danckwerts, R. (1999): Dynamische Visualisierung und Mathematikunterricht: Ein Beispiel. – Vortrag auf der 33. Tagung für Didaktik Mathematik (1. bis 5. März 1999 in Bern)
Laborde, J.M.; Bellemain, F. (1996): Cabri Géomètre II. Windows Version 1.0 – Dallas/USA u. Freising: Texas Instruments. (Deutsche Oberfläche und Bearbeitung des Handbuchs von H. Schumann)
Schumann, H. (1985): Umfangsgleiche Rechtecke. – In: mathematik lehren (11), August., S. 42-45
Schumann, H. (1994): Schulgeometrisches Konstruieren mit dem Computer. – Velten: Becker
Schumann, H. (1998a): Interaktive Arbeitsblätter für das Geometrielernen. – In: Mathematik in der Schule (36), Heft 10, S. 562-569
Schumann, H. (1998b): Geometrische Extremwertaufgaben in dynamischer Behandlung. In: ZDM 30, Heft 6, S. 215-223
Schupp, H. (1996): Regeometrisierung der Schulgeometrie – durch Computer? In: Hischer, H. (Hrsg.): Computer und Geometrie. Neue Chancen für den Geometrieunterricht. – Hildesheim: Franzbecker, S. 16-25.
Schupp, H. (1992): Optimieren – Extremwertbestimmung im Mathematikunterricht.- Mannheim: B.I. Wissenschaftsverlag
Wittmann, E. (1981): Grundlagen des Mathematikunterrichts.- Braunschweig: Vieweg (6. Auflage)
Die verwendeten CabriII-Dateien können von der Homepage des Autors, die sich unter der Internet-Adresse: ph-weingarten.de befindet, heruntergeladen werden.